1611671589-8b32ec633a68274ab2f981b506c8e32e (826555), страница 7
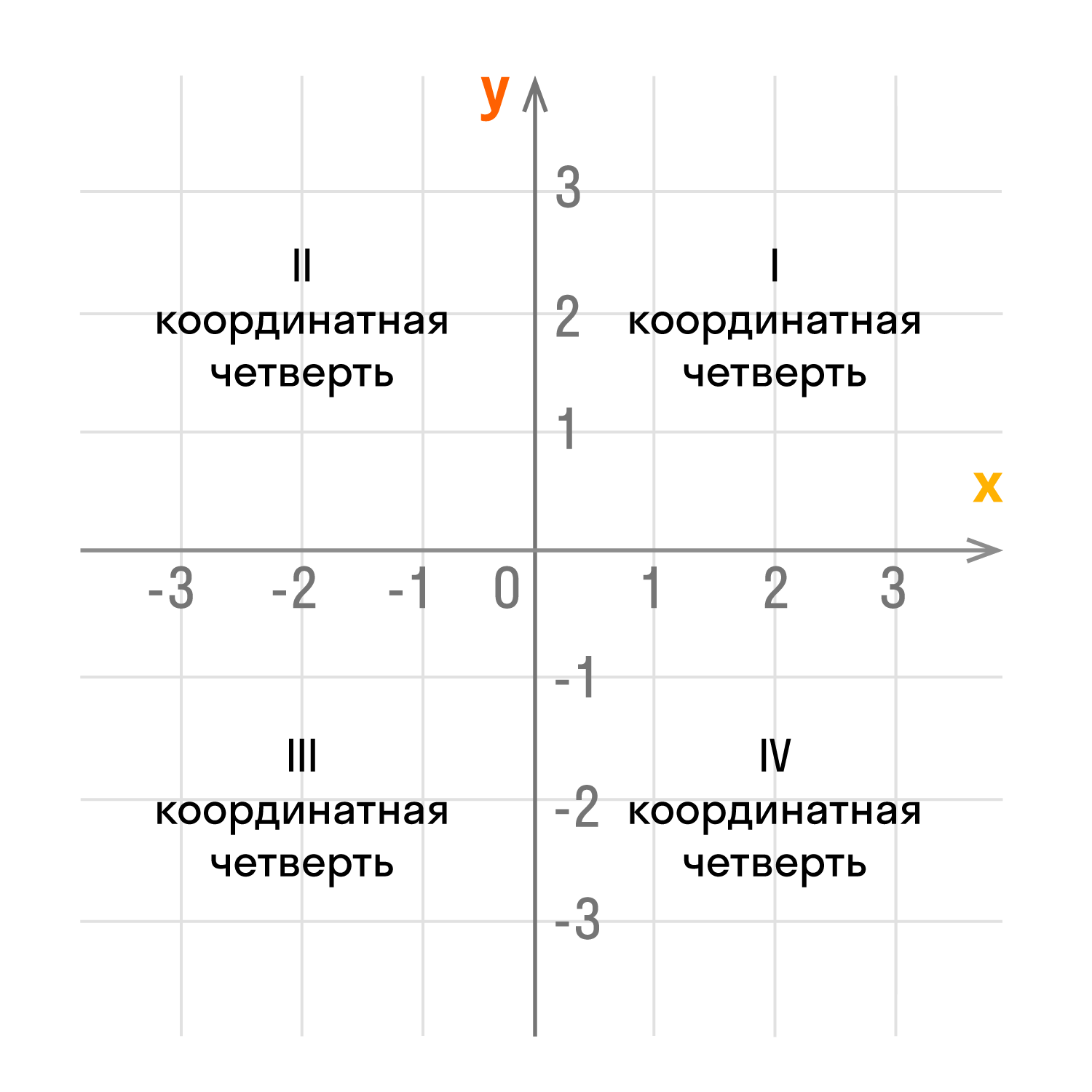
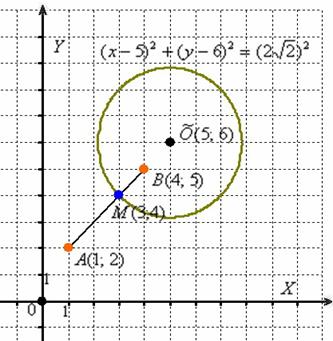
Кривые второго порядка — это геометрическое место точек плоскости, прямоугольные координаты которых удовлетворяют уравнению вида. Считается, что первым занялся изучением кривых второго порядка один из учеников Платона. Основываясь на траекториях отражения света, очертаниях растений и других природных явлениях, он предположил, что если взять две прямые, пересекающихся между собой, и начать вращать их вокруг угла ими же образованного, то получиться косинусовидная поверхность, которая при пересечении другой плоскостью станет образовывать сечение в виде различных геометрических фигур: эллипс, окружность, парабола, гипербола и др.



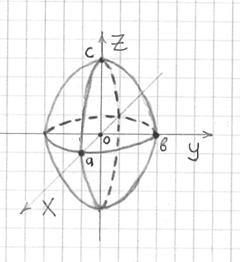
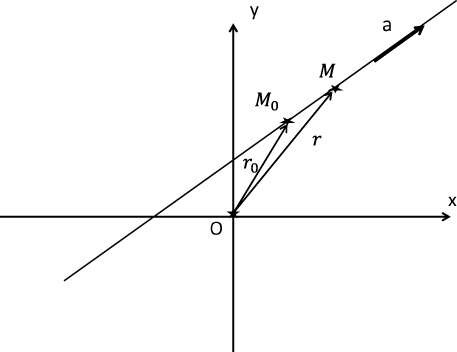
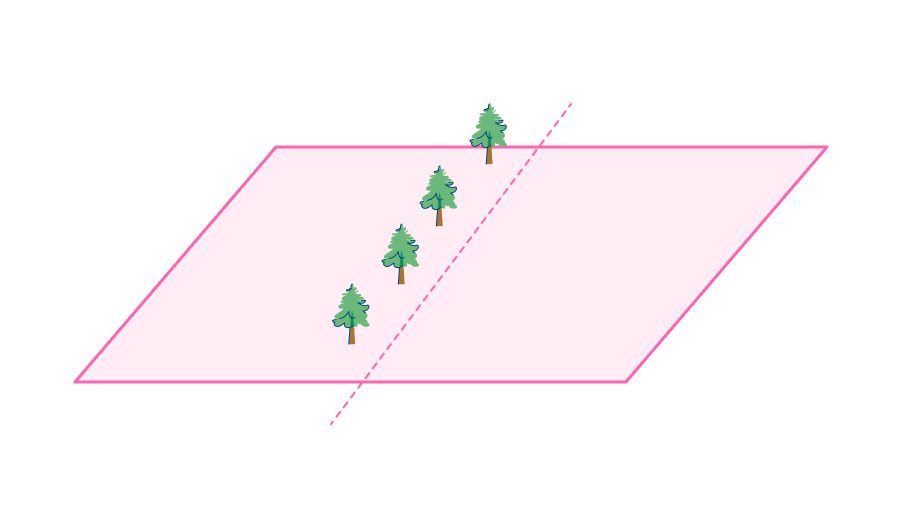



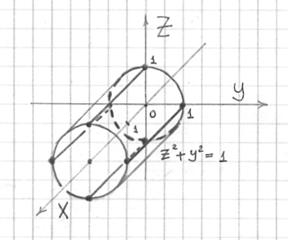
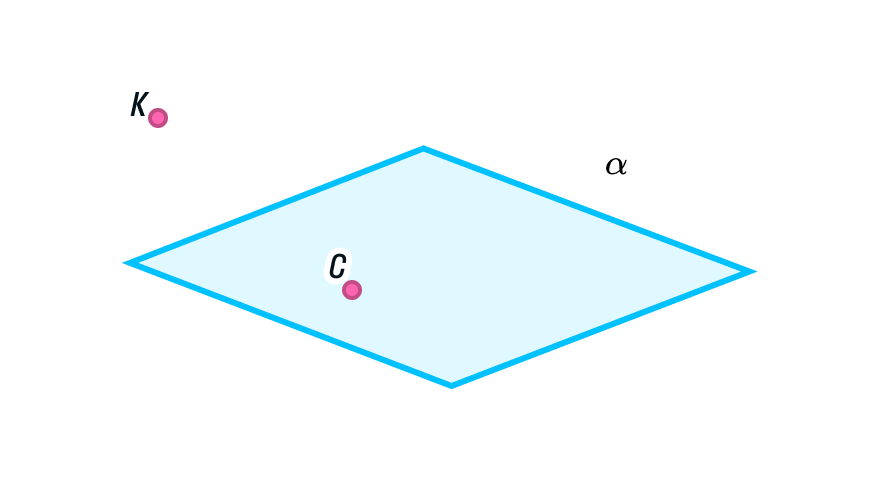
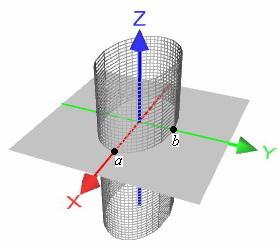
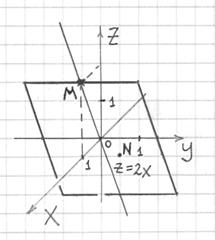
Поверхность второго порядка — геометрическое место точек, декартовы прямоугольные координаты которых удовлетворяют уравнению вида. Поверхность S называется цилиндрической поверхностью с образующей , если для любой точки M0 этой поверхности прямая, проходящая через эту точку параллельно образующей , целиком принадлежит поверхности S. Теорема об уравнении цилиндрической поверхности. Если направляющая цилиндрической поверхности задаётся кривой второго порядка, то такая поверхность называется цилиндрической поверхностью второго порядка.
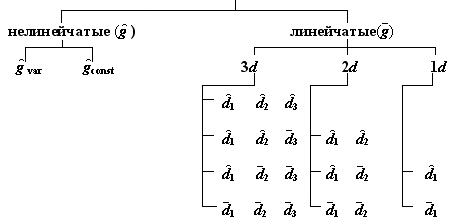


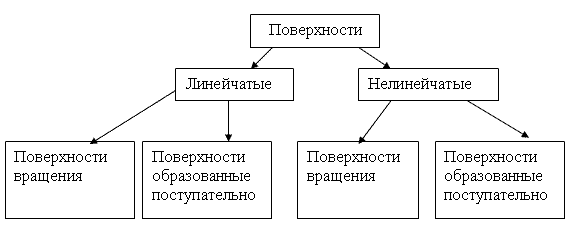
Поверхность второго порядка — геометрическое место точек трёхмерного пространства, прямоугольные координаты которых удовлетворяют уравнению вида. Является частным случаем квадрики. Теорема об уравнении цилиндрической поверхности.